sandwiching a spline

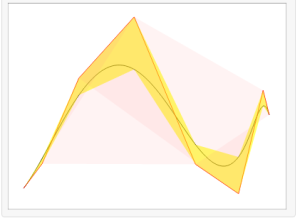
The strong convex hull property says that for a spline of degree , the convex hull of at most control points of a spline contains the point of a spline at parameter . Intersection methods can use this property to rule out certain interections. Union of a convex hulls of consecutive points completely encompass the spline as in the figure below (pink region represents of convex hulls)

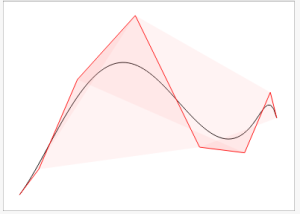
However one finds that such a union often encompasses large areas as in the figure above. In order to better this, we give a simple scheme which only involves evaluation of splines to compute a polygon around a spline which provides a tighter enclosure of the spline, see below:

Let be the control points of the spline and let be its knots. Also let the hat coordinates be the greville abscissae of . We assume that that the the spline we are dealing is clamped at the start and end. The polygon that encloses that spline is determined by ceiling and floor points defined as below:

Now construct a polygon joining the ceiling points at the top and floor points below. In the figure below this is indicated by the yellow region. Clearly, this cages the brutish spline better. It would be fun to work out a proof but for now lets stick with evidence.

You can play with the points below:
Mathematica code

In a sense this is not a fair comparison between convex hull method, since evaluation of a spline is equivalent to knot insertion and a side affect of insertion is that control frame comes closer to the spline, so one would expect that the convex hull of the new control frame would be tighter.